SAT Math Test Review & Prep Guide

SAT Math may seem daunting, but it’s very possible to score well. Understanding what’s on the test, how it works, and what you need to know are the first steps to success. Here’s our SAT Math may seem daunting, but it’s very possible to score well. Understanding what’s on the test, how it works, and what you need to know are the first steps to success. Here’s our guide for everything you will need to know to achieve your goals on the Math sections of the SAT.

SAT Math: Brief Overview

SAT Math Test Structure

Math on the SAT is split into two sections: a no-calculator portion, and a calculator portion. They are, respectively, the third and fourth sections of the test.

The no-calculator section is 25 minutes and 20 questions, and the calculator section is 55 minutes and 38 questions.

Both sections are primarily multiple choice, but include some grid-in questions at their ends. The multiple choice questions each have four answer choices, and the grid-ins, which ask you to write in an answer, are always a non-negative, real number. There is no penalty for incorrect answers.

SAT Math Content

The College Board breaks down the math content on the SAT into four categories: "Heart of Algebra," "Problem Solving and Data Analysis," "Passport to Advanced Math," and "Additional Topics."

Heart of Algebra makes up about a third of the questions and focuses on linear equations and systems of equations. Problem solving and Data Analysis focuses on quantitative literacy, and Passport to Advanced Math requires fluency with more complex equations. Those sections each make up about 28-29% of the math questions. Additional Topics, the smallest category, makes up about 10% of the questions and primarily covers geometry and trigonometry. Students also may be required to answer questions about more advanced topics such as complex numbers and matrices.

Why is SAT Math so hard?

A variety of factors, stemming from both content and form, contribute to the difficulty of SAT Math:

• Questions, even those based on simple concepts, are often formulated to require several steps and cover multiple topics in their solutions.
• Though most of the test covers topics that students have encountered in school, the Problem Solving and Data Analysis and Additional Topics categories deal with potentially unfamiliar concepts.
• The no-calculator portion is designed to deal with less complicated calculations, but requires a deeper conceptual understanding of math topics than students might have needed for their schoolwork.
• The test is timed, so you must be able to work relatively quickly.
• The math sections are at the end of the test, which may challenge your focus and endurance.
  

However, students need not be discouraged. Though some aspects of the test provide a challenge, it is far from insurmountable. As previously mentioned, the test is designed to primarily cover topics that students should have covered in school before, so there aren’t a lot of new concepts to learn. Moreover, while any timed test can feel rushed, the timing on the SAT is more generous than on the ACT, so students who struggle with timing might feel more comfortable with the SAT. Finally, the SAT provides a formula sheet which, though limited in scope, is a helpful safety net for students worried about memorizing certain equations.

What kind of math is on SAT?

The SAT covers topics in algebra, statistics, probability, geometry, trigonometry, and some other advanced topics. The tools, skills, and concepts you should be familiar with include the following:

• Fundamental Algebra
  • You should be able to create, solve, or interpret linear equations, systems of equations, or linear inequalities.
  • You should be able to model situations using linear equations and inequalities
  • You should understand the connections between algebraic and graphical representations of linear equations and inequalities.
• Basic statistics, data analysis, and probability
  • You should be able to read tables and derive summarizing statistics and conditional probabilities.
  • You should be able to evaluate data collection methods.
  • You should be able to solve problems involving percentages, unit conversions, ratios, rates, and proportions.
• Advanced Algebra
  • You should be able to create, solve, and interpret quadratic, exponential, radical, and rational functions or equations.
  • You should be able to recognize and formulate equivalences between rational exponents and radicals and between negative exponents and fractions.
  • You should be able to add, subtract, multiply, and factor polynomial expressions, including those with rational coefficients.
  • You should understand the relationship between algebraic and graphical representations of nonlinear functions, such as the relationship between zeros and factors of polynomials.
• Trigonometry, Planar Geometry, and Coordinate Geometry
  • You should be able to solve problems using area and volume formulas.
  • You should be able to use trigonometric ratios, the Pythagorean Theorem, and concepts of congruence and similarity to solve for side lengths and angle measures of triangles.
  • You should be able to convert between radians and degrees, and to know the trigonometric ratios of common angle measures found on the unit circle.
  • You should be able to use central angle measurements to find arc lengths and sector areas of circles.
  • You should understand and be able to formulate the equation representing a circle in the coordinate plane.
• Misc.
  • You should be able to add, subtract, multiply, divide, simplify complex numbers.
  • You should be able to add and subtract matrices.

What math is most important for SAT?

Algebra is by far the area of math that covers the most questions on the SAT. The Heart of Algebra and Passport to Advanced Math categories cover basic and advanced algebra, respectively, and together cover over 60% of the Math sections. The next most important area is data analysis and probability, which covers close to 30% of the Math sections. Focusing on these areas will have the greatest impact on improving your SAT Math score.

What to study for SAT Math?

Studying for standardized tests is both about mastering content and building familiarity with the format. Make sure you’re adept at the content areas previously listed, and take practice tests to identify any areas of weakness. As previously mentioned, mastering both foundational and advanced algebra skills is crucial to performing well. That being said, it’s not just enough to study the content. Your practice should include timed sessions, to make sure you’re able to keep pace with the test. You should match other restrictions of the test in your practice, too: don’t use a calculator for the calculator portion, and don’t let yourself have access to formulas that won’t be provided on the formula sheet.

SAT Math Formulas and Definitions to memorize

Though the SAT provides you with some formulas, it’s useful to know at least some of those formulas by heart. Moreover, there are several others that are crucial to know with ease to achieve high scores.

Careful! It’s not just enough to memorize these formulas: you need to know how and when to use them, and what the variables represent.

Circles

Area of a circle: $A = πr^2$

Circumference of a cirlce: $2πr$

Equation of a circle: $(x- h)^2 + (y-k)^2 = r^2$

Length of an arc: $\frac{radian measure of central angel}{2π} = \frac{degree measure of central radian}{360} = \frac{length of arc}{2πr}$

Area of a sector: $\frac{radian measure of central angel}{2π} = \frac{degree measure of central radian}{360} = \frac{area of sector}{πr^2}$

Triangles

Area of a triangle: $A = \frac{1}{2}bh$

The Pyhtagorean Theorem: $a^2 + b^2 = c^2$

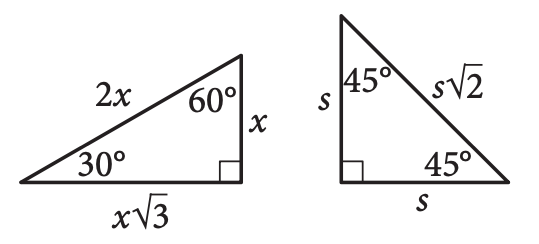
Special right triangles:

Solids

Volume of a rectangular solid: $l x w x h$

Volume of a cylinder: $πr^2h$

Lines and Points

Slope formula, given two points: $\frac{\Delta y}{\Delta x} =$$\frac{y_1-y_2}{x_1-x_2}$

Slope-intercept form: $y = mx + b$ (and make sure you know what m and b represent)

Midpoint Formula: The midpoint between points $(x_1, y_1)$ and $(x_2, y_2)$ is $(\frac{x_1 + x_2}{2}$, $, \frac{y_1 + y_2}{2})$

Distance formula: $d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$ (even better, see if you can derive this using the Pythagorean theorem!)

Binomials and Quadratics

Quadratic Equations: If $ax^2 + bx + c = 0$, then $x = \frac{-b ± \sqrt{b^2 - 4ac}}{2a}$​​.

Difference of squares: $a^2 - b^2 = (a + b)(a - b)$

Squaring a binomial: $(a+b)^2 = a^2 + 2ab + b^2$

Exponents and Radicals

• $x^{a}x^{b} = x^{a + b}$
• $(x^a)^b = x^{ab}$
• $x^{-a} = \frac{1}{x^a}$
• $x^{a/b} = \sqrt[b]{x^a}$
• $x^0 = 1$

Data analysis and probability

Mean: $\frac{sum of terms}{number of terms}$

Median: middle value (when you put the terms in order)

Mode: most frequent value

Probability of an outcome: $\frac{number of desired outcomes}{total number of possible outcomes}$

Trigonometry

SOHCAHTOA:

• $sin (x) = opp/hyp$
• $cos (x) = adj/hyp$
• $tan (x) = opp/adj$

$sinx = cosy$ when $x + y = 90\degree$

SAT Math Tips from Ivy Tutors Network

1. Practice using problems from official tests and study guides.

Though you’ve likely encountered most content from the test in your schoolwork, it’s important to not just rely on your school materials for study. The College Board formulates questions in particular, and sometimes confusing, ways. Practicing from official tests and study guides will help you understand what SAT questions are asking for, which is key to performing well.

2. Make sure you understand what’s going on conceptually

The no-calculator section in particular tests your conceptual understanding more than your computational prowess. It won’t be enough just to know the steps to take to solve questions you might have seen in school; you need to understand why those are the correct steps to be able to adapt to SAT questions.

3. Memorize equations, but understand them first.

There are several equations that will be useful to know by heart. That being said, it’s important to know what those equations represent, how they can be used, and why they are formulated the way they are in order to use them properly. Moreover, understanding the equations will make them easier to remember!

4. Take full-lenth, timed practice tests.

In order to do well on standardized tests such as the SAT, you need to be able to answer the questions within the time and format restrictions of the test. The best way to build speed, endurance, and comfortability with these restrictions is to simulate a testing environment by taking timed practice tests. Building endurance is particularly important for the math sections, which are at the end of the SAT. IVY offers diagnostic and mock testing services for all our clients, including comprehensive score reports.

5. Set score goals.

As you are studying, it’s important to set goals. This will help you know if you’re on the right track throughout your studying journey, and can help motivate and guide your approach to studying. Ultimately, students are taking the SAT largely as part of their college applications, so you want to make sure you know what scores the colleges to which you are applying are expecting to see.

6. Make a study plan.

Effective studying doesn’t just involve having a basic understanding of all concepts covered on the test. The best approaches thoroughly attack the highest priority subjects first, and systematically evaluate weaknesses to guide your practice. Having a plan will help to ensure that you cover all your bases, and will give you a guideline to judge if you’re on track along the way.

7. Have a realistic and effective timeline.

The best way to learn anything is to study in short, frequent sessions over a sufficiently long period of time. At IVY, we recommend studying for at least three months before taking an official test, and many students plan for longer than that. There’s a lot to master on the SAT, so make sure you give yourself enough time and practice frequently enough to give yourself the best chance of success!

8. Work with a tutor.

An experienced tutor can help you with every step of your studying journey, not only helping you to learn content but also helping you build a study plan, set goals, and evaluate your progress along the way. Our SAT tutors at IVY are experts at guiding students towards success on the SAT and other standardized tests.guide for everything you will need to know to achieve your goals on the Math sections of the SAT.

SAT Math: Brief Overview

SAT Math Test Structure

Math on the SAT is split into two sections: a no-calculator portion, and a calculator portion. They are, respectively, the third and fourth sections of the test.

The no-calculator section is 25 minutes and 20 questions, and the calculator section is 55 minutes and 38 questions.

Both sections are primarily multiple choice, but include some grid-in questions at their ends. The multiple choice questions each have four answer choices, and the grid-ins, which ask you to write in an answer, are always a non-negative, real number. There is no penalty for incorrect answers.

SAT Math Content

The College Board breaks down the math content on the SAT into four categories: "Heart of Algebra," "Problem Solving and Data Analysis," "Passport to Advanced Math," and "Additional Topics."

Heart of Algebra makes up about a third of the questions and focuses on linear equations and systems of equations. Problem solving and Data Analysis focuses on quantitative literacy, and Passport to Advanced Math requires fluency with more complex equations. Those sections each make up about 28-29% of the math questions. Additional Topics, the smallest category, makes up about 10% of the questions and primarily covers geometry and trigonometry. Students also may be required to answer questions about more advanced topics such as complex numbers and matrices.

Why is SAT Math so hard?

A variety of factors, stemming from both content and form, contribute to the difficulty of SAT Math:

• Questions, even those based on simple concepts, are often formulated to require several steps and cover multiple topics in their solutions.
• Though most of the test covers topics that students have encountered in school, the Problem Solving and Data Analysis and Additional Topics categories deal with potentially unfamiliar concepts.
• The no-calculator portion is designed to deal with less complicated calculations, but requires a deeper conceptual understanding of math topics than students might have needed for their schoolwork.
• The test is timed, so you must be able to work relatively quickly.
• The math sections are at the end of the test, which may challenge your focus and endurance.
  

However, students need not be discouraged. Though some aspects of the test provide a challenge, it is far from insurmountable. As previously mentioned, the test is designed to primarily cover topics that students should have covered in school before, so there aren’t a lot of new concepts to learn. Moreover, while any timed test can feel rushed, the timing on the SAT is more generous than on the ACT, so students who struggle with timing might feel more comfortable with the SAT. Finally, the SAT provides a formula sheet which, though limited in scope, is a helpful safety net for students worried about memorizing certain equations.

What kind of math is on SAT?

The SAT covers topics in algebra, statistics, probability, geometry, trigonometry, and some other advanced topics. The tools, skills, and concepts you should be familiar with include the following:

• Fundamental Algebra
  • You should be able to create, solve, or interpret linear equations, systems of equations, or linear inequalities.
  • You should be able to model situations using linear equations and inequalities
  • You should understand the connections between algebraic and graphical representations of linear equations and inequalities.
• Basic statistics, data analysis, and probability
  • You should be able to read tables and derive summarizing statistics and conditional probabilities.
  • You should be able to evaluate data collection methods.
  • You should be able to solve problems involving percentages, unit conversions, ratios, rates, and proportions.
• Advanced algebra
  • You should be able to create, solve, and interpret quadratic, exponential, radical, and rational functions or equations.
  • You should be able to recognize and formulate equivalences between rational exponents and radicals and between negative exponents and fractions.
  • You should be able to add, subtract, multiply, and factor polynomial expressions, including those with rational coefficients.
  • You should understand the relationship between algebraic and graphical representations of nonlinear functions, such as the relationship between zeros and factors of polynomials.
• Trigonometry, Planar Geometry, and Coordinate Geometry
  • You should be able to solve problems using area and volume formulas.
  • You should be able to use trigonometric ratios, the Pythagorean Theorem, and concepts of congruence and similarity to solve for side lengths and angle measures of triangles.
  • You should be able to convert between radians and degrees, and to know the trigonometric ratios of common angle measures found on the unit circle.
  • You should be able to use central angle measurements to find arc lengths and sector areas of circles.
  • You should understand and be able to formulate the equation representing a circle in the coordinate plane.
• Misc.
  • You should be able to add, subtract, multiply, divide, simplify complex numbers.
  • You should be able to add and subtract matrices.

What math is most important for SAT?

Algebra is by far the area of math that covers the most questions on the SAT. The Heart of Algebra and Passport to Advanced Math categories cover basic and advanced algebra, respectively, and together cover over 60% of the Math sections. The next most important area is data analysis and probability, which covers close to 30% of the Math sections. Focusing on these areas will have the greatest impact on improving your SAT Math score.

What to study for SAT Math?

Studying for standardized tests is both about mastering content and building familiarity with the format. Make sure you’re adept at the content areas previously listed, and take practice tests to identify any areas of weakness. As previously mentioned, mastering both foundational and advanced algebra skills is crucial to performing well. That being said, it’s not just enough to study the content. Your practice should include timed sessions, to make sure you’re able to keep pace with the test. You should match other restrictions of the test in your practice, too: don’t use a calculator for the calculator portion, and don’t let yourself have access to formulas that won’t be provided on the formula sheet.

SAT Math Formulas and Definitions to memorize

Though the SAT provides you with some formulas, it’s useful to know at least some of those formulas by heart. Moreover, there are several others that are crucial to know with ease to achieve high scores.

Careful! It’s not just enough to memorize these formulas: you need to know how and when to use them, and what the variables represent.

Circles

Area of a circle: $A = πr^2$

Circumference of a cirlce: $2πr$

Equation of a circle: $(x- h)^2 + (y-k)^2 = r^2$

Length of an arc: $\frac{radian measure of central angel}{2π} = \frac{degree measure of central radian}{360} = \frac{length of arc}{2πr}$

Area of a sector: $\frac{radian measure of central angel}{2π} = \frac{degree measure of central radian}{360} = \frac{area of sector}{πr^2}$

Triangles

Area of a triangle: $A = \frac{1}{2}bh$

The Pyhtagorean Theorem: $a^2 + b^2 = c^2$

Special right triangles:

Solids

Volume of a rectangular solid: $l x w x h$

Volume of a cylinder: $πr^2h$

Lines and Points

Slope formula, given two points: $\frac{\Delta y}{\Delta x} =$$\frac{y_1-y_2}{x_1-x_2}$

Slope-intercept form: $y = mx + b$ (and make sure you know what m and b represent)

Midpoint Formula: The midpoint between points $(x_1, y_1)$ and $(x_2, y_2)$ is $(\frac{x_1 + x_2}{2}$, $, \frac{y_1 + y_2}{2})$

Distance formula: $d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$ (even better, see if you can derive this using the Pythagorean theorem!)

Binomials and Quadratics

Quadratic Equations: If $ax^2 + bx + c = 0$, then $x = \frac{-b ± \sqrt{b^2 - 4ac}}{2a}$​​.

Difference of squares: $a^2 - b^2 = (a + b)(a - b)$

Squaring a binomial: $(a+b)^2 = a^2 + 2ab + b^2$

Exponents and Radicals

• $x^{a}x^{b} = x^{a + b}$
• $(x^a)^b = x^{ab}$
• $x^{-a} = \frac{1}{x^a}$
• $x^{a/b} = \sqrt[b]{x^a}$
• $x^0 = 1$

Data analysis and probability

Mean: $\frac{sum of terms}{number of terms}$

Median: middle value (when you put the terms in order)

Mode: most frequent value

Probability of an outcome: $\frac{number of desired outcomes}{total number of possible outcomes}$

Trigonometry

SOHCAHTOA:

• $sin (x) = opp/hyp$
• $cos (x) = adj/hyp$
• $tan (x) = opp/adj$

$sinx = cosy$ when $x + y = 90\degree$

SAT Math Tips from Ivy Tutors Network

1. Practice using problems from official tests and study guides.

Though you’ve likely encountered most content from the test in your schoolwork, it’s important to not just rely on your school materials for study. The College Board formulates questions in particular, and sometimes confusing, ways. Practicing from official tests and study guides will help you understand what SAT questions are asking for, which is key to performing well.

2. Make sure you understand what’s going on conceptually

The no-calculator section in particular tests your conceptual understanding more than your computational prowess. It won’t be enough just to know the steps to take to solve questions you might have seen in school; you need to understand why those are the correct steps to be able to adapt to SAT questions.

3. Memorize equations, but understand them first.

There are several equations that will be useful to know by heart. That being said, it’s important to know what those equations represent, how they can be used, and why they are formulated the way they are in order to use them properly. Moreover, understanding the equations will make them easier to remember!

4. Take full-lenth, timed practice tests.

In order to do well on standardized tests such as the SAT, you need to be able to answer the questions within the time and format restrictions of the test. The best way to build speed, endurance, and comfortability with these restrictions is to simulate a testing environment by taking timed practice tests. Building endurance is particularly important for the math sections, which are at the end of the SAT. IVY offers diagnostic and mock testing services for all our clients, including comprehensive score reports.

5. Set score goals.

As you are studying, it’s important to set goals. This will help you know if you’re on the right track throughout your studying journey, and can help motivate and guide your approach to studying. Ultimately, students are taking the SAT largely as part of their college applications, so you want to make sure you know what scores the colleges to which you are applying are expecting to see.

6. Make a study plan.

Effective studying doesn’t just involve having a basic understanding of all concepts covered on the test. The best approaches thoroughly attack the highest priority subjects first, and systematically evaluate weaknesses to guide your practice. Having a plan will help to ensure that you cover all your bases, and will give you a guideline to judge if you’re on track along the way.

7. Have a realistic and effective timeline.

The best way to learn anything is to study in short, frequent sessions over a sufficiently long period of time. At IVY, we recommend studying for at least three months before taking an official test, and many students plan for longer than that. There’s a lot to master on the SAT, so make sure you give yourself enough time and practice frequently enough to give yourself the best chance of success!

8. Work with a tutor.

An experienced tutor can help you with every step of your studying journey, not only helping you to learn content but also helping you build a study plan, set goals, and evaluate your progress along the way. Our SAT tutors at IVY are experts at guiding students towards success on the SAT and other standardized tests.